[시계열 분석] 자기 상관

카테고리 없음

yennle 2022. 10. 10. 03:06

728x90

위 글에서 자기 상관을 다뤘다.

조금 더 깊게 다뤄보고자 공부한 내용을 정리하고자 한다.

보통 두 확률변수에 대한 상관계수를 구할 때는 아래 식을 사용한다.

그리고 -1과 1 사이의 값으로 표현되어 0에 가까우면 변수 간의 관계가 없다고 할 수 있고,

1에 가까우면 양의 상관관계, -1에 가까우면 음의 상관관계를 가진다고 할 수 있다.

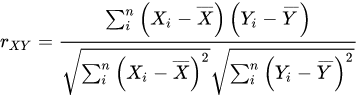
자기 상관계수를 구할 때에는 위의 식과 비슷하지만,

시점의 차이를 이용해 시점마다의 상관계수를 구할 수 있다.

식은 아래와 같다.

~~분모가 왜 저렇게 되는지는 못 찾았다. 분포가 같아서 그런가?~~

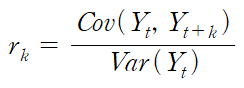
시차마다 자기 상관계수를 구해서 그래프를 그리면 아래와 같은 그래프를 그릴 수 있다.

비슷한 패턴을 보이는 것은 계절성 때문이다.

더빈-왓슨 통계량은 종속변수의 오차에 대한 1차 자기상관관계를 의미한다.

(더빈-왓슨 통계량으로 확인할 수 있는 것은 1차 자기상관관계에 국한됨.)

데이터가 일정한 시간단위로 누적된 형태일 경우에 종속변수는 독립변수에 영향을 받는 것이 아니라

종속변수의 전 시차에 영향을 받을 수 있다.

회귀분석을 실행할 때 자기상관관계가 나타난다면 이것은 시계열 분석으로 방향을 틀어야 한다.

더빈-왓슨 통계량을 구하는 식을 아래와 같다.

위의 식을 풀어보면 아래 사진과 같아진다.

아래 식의 rho는 자기상관계수를 의미한다.

따라서, 더빈-왓슨 통계량은 0에서 4의 값을 가지며,

2에 가까울수록(상관계수가 0에 가까울수록) 1차 자기상관관계가 없는 것이라고 할 수 있고,

0에 가까울수록(상관계수가 1에 가까울수록) 양의 1차 자기상관관계,

4에 가까울수록(상관계수가 -1에 가까울수록) 음의 1차 자기상관관계가 있다고 할 수 있다.

[참고]

728x90