Just Fighting
[시계열 분석] 시계열 데이터 탐색법 본문
< 정상성 >
정상성 : 평균과 분산이 일정하고, 특정 추세를 가지지 않는 것.
정상 시계열은 측정된 시계열의 안정적인 상태를 반영
정상이라고 판단하는 것보다 정상이 아닌 것을 배제하는 것이 훨씬 수월
아래 사진은 정상이 아닌 시계열의 예시이다.
시간에 따라 데이터의 평균과 분산이 변하고,계절성의 증거도 확인 가능함.

로그와 제곱근 등으로 시계열을 정상화할 수 있음.
이 둘은 특히 분산이 변화할 때 사용됨.
추세는 차분을 구하여 제거하는 것이 일반적.
< 윈도 함수 적용 >
- 롤링 윈도 : 특정 크기(10분, 1시간, 1일과 같이 기간을 의미)를 유지한 채 측정 단위 시간별로 이동하면서 분석하는 방법
- 확장 윈도 : 처음 시작 시점을 고정한 채로, 누적해서 데이터를 분석

< 자기상관 >
자기상관 : 어떤 신호와 자신을 지연 함수로 시간상 지연 이동한 신호 간의 상관관계.
시차에 대한 함수로 관측치 사이의 유사성을 구하는 것.
서로 다른 시점의 데이터 간 선형적 연관성 정도를 시차에 대한 함수로 알 수 있게 함. => 자기상관함수(ACF)

시차가 0일 때의 상관계수는 1, 시차가 1일 때의 상관계수는 0.5, 시차가 2일 때의 상관계수는 -0.5가 된다.
- ACF의 주기함수는 원래 과정과 동일한 주기성을 가짐.
- 주기함수들의 합의 자기 상관은 각 개별함수에 대한 자기 상관의 합임.
- 시차가 0일 때, 모든 시계열의 자기상관계수는 1.
- 백색잡음 데이터에 대해서 0이 아닌 모든 시차에서의 자기상관은 0에 가까움.
- 양과 음의 시차에 관해서 대칭을 이룸.
- 0이 아닌 유효한 ACF 추정을 결정하는 통계적인 규칙은 +/-1.96*sqrt(n)의 임계영역을 사용하는 것.

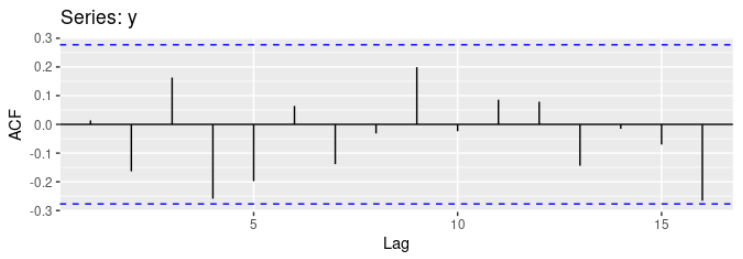
=> ACF는 적절한 정도의 시간 규모를 위한 윈도 길이를 얻는데 유용함.
편자기상관 : 자신에 대한 그 시차의 편상관. 이 때, 두 시점 사이에 존재하는 모든 정보를 고려함.
"두 시점 사이의 정보를 처리한다."
=> 많은 조건부 상관관계를 계산하고, 전체 상관관계로부터 계산된 조건부 상관관계들을 빼야한다는 의미.
- 편자기상관함수(PACF)는 ACF와 대조적.
- PACF는 어떤 데이터가 유용한 정보를 가지고, 어떤 데이터가 단기간의 고조파인지를 보여줌.
- 임계영역은 ACF와 동일하게 +/-1.96*sqrt(n)

< 허위상관 >
전혀 상관이 없는 데이터들이 비슷한 추세를 보이고 있는 것.
허위상관을 나타내는 시계열의 일반적인 특징
- 계절성 : 핫도그 소비와 익사(여름) 사이의 허위상관
- 시간이 지나면서 변한 데이터의 수준이나 경사의 이동(무의미하게 높은 상관관계를 가진 아령처럼 생긴 분포도 생성)
- 누적합계(일부산업에서는 모델이나 상관관계를 더 좋아보이게 만들기 위해 속임수로 사용)
@@ 공적분 @@
공적분은 두 시계열 사이의 진짜 관계를 지칭함.
두 시계열 사이에 높은 상관관계가 관측되면 공적분인지 허위상관인지 구별하기 어려움
그러나, 허위상관은 어떤 관계가 없어도 되지만, 공적분은 서로 밀접한 관련성을 가짐을 의미함.
[참고]
에일린 닐슨, 「실전 시계열 분석」, 박찬성, 한빛미디어(2021)
