Just Fighting
[프로그래머스] 멀쩡한 사각형 본문
https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
<문제 설명>
가로 Wcm, 세로 Hcm인 직사각형 종이가 있고, 1x1cm인 격자가 그려져 있다.
격자를 따라 1x1cm인 정사각형으로 잘라 이용하려고 했는데, 종이가 대각선으로 잘려 있다.
이 때, 사용할 수 있는 정사각형의 개수를 구하여라.

<시행착오>
처음에는 예시만 보고 단순하게 세로줄 하나에 (h/w의 올림한 값)과 같은 개수의 사각형을 사용하지 못한다고 생각했다.
그래서 h, w중에 길이가 짧은 값을 a라고 했을때,
w * h - a * math.ceil(h/w)
을 이용해서 풀었지만, 풀리지 않았다.
두번째로는 함수를 이용했다.
y절편이 h이고, 기울기가 h/w인 함수를 만들어 각 1~w까지의 함수값을 구하고 모두 합한 뒤,
2배 한 값을 리턴했다. 하지만 이것도 안됐다^^
<문제 풀이>
문제에 패턴이 2x3인 직사각형이 4번 반복된다는 것에 유의했고, 4는 8과 12의 최대공약수임을 알았다.
그러나 어떻게 사용해야할지에 대해 갈피를 잡지 못했다.
다른 사람들의 풀이를 여러 개 보면서 문제 풀이 방법을 이해할 수 있었다.
일단 기본적으로 상하좌우로 움직여 격자 무늬 왼쪽 상단에서 오른쪽 하단으로 가기 위해
거쳐야하는 정사각형의 최소 개수는 '(가로) + (세로) - 1' 이다. (사이드로 가든 지그재그로 가든 다 같음)
이는 "직선이 꼭지점을 지나지 않는 경우"에 거치는 정사각형의 개수와 동일하다.
따라서 위의 예시에서는 이 식이 성립하지 않는다.
하지만 위의 예시 속 패턴이 반복되는 2x3인 직사각형에 대해서는 성립된다! (얘는 직선이 꼭지점을 지나지 않으니까)
이 때 '(가로) + (세로) - 1'에서 '1'은 (가로)와 (세로)의 최대공약수라고 할 수 있다.
 |
 |
w와 h의 최대공약수를 gcd(w,h)라고 하면,
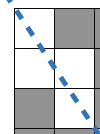
두번째 사진에 대해 w/gcd(w,h) + h/gcd(w,h) - 1 로 표현할 수 있다.
위에서 말했듯이 두번째 사진의 패턴이 첫번째 사진에서 4번, 즉 최소공배수만큼 나타나기 때문에
첫번째 사진에 대해서는 w + h - gcd(w,h) 로 표현할 수 있다.
따라서 w * h - (w + h - gcd(w,h)) 를 리턴하면 된다.
def solution(w,h):
a,b = (w,h) if w > h else (h,w) # 큰 수 찾기
while b != 0: # 최대공약수 찾기
r = a % b # 최대공약수는 a
a = b
b = r
return w*h - (w+h-a)
<풀이 개선>
파이썬에는 최대공약수를 구하는 함수가 있다..!
import math
def solution(w,h):
return w*h-(w+h-math.gcd(w,h))
진짜 죽어도 이해 안되다가
결국 깨달았다 쾌감,,,
'Algorithm > 코딩테스트 연습' 카테고리의 다른 글
| [프로그래머스] 기능개발 (0) | 2022.02.05 |
|---|---|
| [프로그래머스] 124 나라의 숫자 (0) | 2022.02.04 |
| [프로그래머스] 실패율 (0) | 2022.01.31 |
| [프로그래머스] 순위 검색 (0) | 2022.01.26 |
| [프로그래머스] 괄호 변환 (0) | 2022.01.25 |




