Just Fighting
[시계열 분석] 자기회귀 모델(AR) 본문
다중 회귀 모델에서는 독립변수의 선형 조합을 이용해 종속변수를 예측했다.
그렇다면 시계열 분석에서 자기회귀 모델은 변수의 과거 값의 선형 조합을 이용해 특정 시점의 값을 예측한다.
기본 식은 다음과 같이 표현할 수 있다.
아래 식은 AR(1)을 의미하며, t-1시점의 값이 t시점에 영향을 미친다는 의미가 된다.
하나의 원인 변수만 지닌 간단한 선형회귀와 동일한 형식을 가진다.

차수 p의 자기회귀 모델을 다음과 같다.

이때, 오차항은 평균이 0이고 분산이 시그마 제곱인 정규분포를 따른다. $\varepsilon \sim N(0,sigma^2)$
가정
- $\varepsilon \sim N(0,sigma^2)$
- $y$와 $\varepsilon$는 독립
- y는 정상성을 가짐
< 평균 >
AR(1)을 이용하여, 함수의 평균과 분산을 계산해보자.
시계열 분석의 핵심은 정상성이기 때문에, 과정이 정상이라고 가정하자.
정상성의 가정으로부터 과정의 기대값은 모든 시간에서 동일해야 한다.

이고

이므로

이 성립하고

기대값을 위와 같이 표현할 수 있다.
위의 mu값의 식을 이용하면 아래와 같이 식을 바꿔 작성할 수 있다.
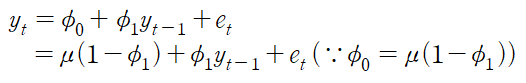
mu를 좌항으로 옮기고 정리하면 아래와 같이 정리할 수 있으며,
$y_t - \mu$는 오차항들에 대한 선형함수라고 할 수 있다.

< 분산 >
분산을 구해보자.
분산은 아래와 같이 구할 수 있다.

다시 정리하면 분산은 아래와 같이 정리할 수 있다.

이 때, $Var(y_t) >= 0$이므로 $-1<\phi_1<1$ 이라는 것을 알 수 있다.
< ACF >
자기상관함수를 구해보자.
먼저 평균을 0이라고 가정해야 한다.


위의 공분산 식을 이용하여 $k=1$일 때의 공분산을 구하면

이므로 아래 식을 완성할 수 있다.

$r_h$와 $r_{h-1}$의 관계는 아래 식과 같이 표현할 수 있다.



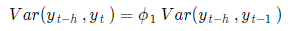
따라서, $Cov(Y_t, Y_{t+k}) = {\phi_1}^k Cov(Y_t, Y_t) = {\phi_1}^k Var(Y_t)$ 이므로 아래 식과 같이 표현할 수 있다.

[참고]
에일린 닐슨, 「실전 시계열 분석」, 박찬성, 한빛미디어(2021)
https://otexts.com/fppkr/AR.html
https://zephyrus1111.tistory.com/102
http://kanggc.iptime.org/grad-em/Lec3/Lec-3.pdf
https://datalabbit.tistory.com/117
https://online.stat.psu.edu/stat510/lesson/1/1.2
