[최적화] ortools 연습하기
최적화의 목표는 가능한 많은 해법 세트 중에서 문제에 대한 최적의 해결책을 찾는 것.
구글의 ortools를 이용해 최적화 문제를 푸는 방법을 익혀보자.
선형문제에 사용하는 솔버인 GLOP를 사용해 최적화 문제를 해결하는 방법을 연습했다.
2가지 방법이 눈에 띄어 함께 테스트해보았다.
1. Constraint와 Objective 사용
https://developers.google.com/optimization/introduction/python?hl=ko

먼저 라이브러리를 가져온다.
# 라이브러리 가져오기
from ortools.init.python import init
from ortools.linear_solver import pywraplp
문제 해결자(솔버)를 선언하고, 풀고자하는 문제의 변수를 생성한다.
0~1의 값을 가지는 x라는 변수와 0~2의 값을 가지는 y라는 변수를 생성한다.
solver.NumVariables()를 실행하면 현재 변수의 개수를 확인할 수 있다.
# 문제 해결자 선언
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver :
print("Could not create solver GLOP")
# 변수 생성
x_var = solver.NumVar(0, 1, 'x')
y_var = solver.NumVar(0, 2, 'y')
print('Number of variables = ', solver.NumVariables())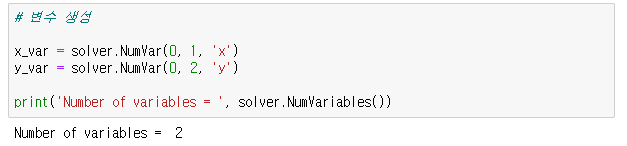
제약조건을 정의한다.
Constraint()함수를 이용해 ct라는 값이 2보다 작은 값임을 정의한다.
그리고 각 항의 계수를 SetCoefficient()로 정의해준다.
NumConstraints()로 제약조건의 개수도 확인 가능하다.
# 제약조건 정의
infinity = solver.infinity()
# 선형 제약조건 x + y <= 2
constraint = solver.Constraint(-infinity, 2, "ct")
constraint.SetCoefficient(x_var, 1)
constraint.SetCoefficient(y_var, 1)
print("Number of constraints =", solver.NumConstraints())
다음으로는 목적함수를 정의해준다.
목적함수는 $3x+y$
Objective()함수와 SetCoefficient()를 이용해서 정의한다.
그리고 목적함수를 최대화하는 것이 목표이기 때문에 SetMaximization()를 실행해주면 된다.
# 목적함수 정의
objective = solver.Objective()
objective.SetCoefficient(x_var, 3)
objective.SetCoefficient(y_var, 1)
objective.SetMaximization()
마지막으로 솔버를 호출하고, 결과를 표시한다.
# 솔버 호출, 결과 표시
result_status = solver.Solve()
if result_status != pywraplp.Solver.OPTIMAL:
print('이 문제는 최적의 해를 가질 수 없음')
if result_status == pywarplp.Solver.FEASIBLE:
print('잠재적으로 최적에 가까운 해를 찾았음')
else:
print('해를 찾지 못함.')
print("Solution:")
print("Objective value =", objective.Value())
print("x =", x_var.solution_value())
print("y =", y_var.solution_value())
2. 조금 더 쉬운 버전
https://developers.google.com/optimization/lp/lp_example?hl=ko

다른 부분은 전부 위의 방식과 동일하지만, 제약조건과 목표함수 정의 부분이 조금 더 단순하다.
위에서는 계수를 설정해줘야 했지만, 이 버전은 수식을 넣어주면 된다.
함수는 Add(). 제약조건을 추가한다는 의미의 함수다.
# 제약조건 정의
solver.Add(x + 2 * y <= 14)
solver.Add(3 * x - y >= 0)
solver.Add(x - y <= 2)
print("Number of constraints =", solver.NumConstraints())
목표함수 정의도 굉장히 단순하다.
목표함수를 정의하지 않고, Maximize()라는 함수로 쉽게 문제를 풀 수 있다.
# 목표함수 정의
solver.Maximize(3 * x + 4 * y)
예제 : 오염된 식단문제
https://developers.google.com/optimization/lp/stigler_diet?hl=ko
영양소의 최소 요건을 만족하면서 재료값을 가장 적게 사용할 수 있는 최적화 문제다.
칼로리만 예를 들어본다면 다음과 같다.
$ (밀가루 양) * (밀가루 칼로리) + (마카로니 양) * (마카로니 칼로리) + \cdots >= 3000 $
이 제약조건이 아래 영양소 목록별로 존재한다고 보면 된다.

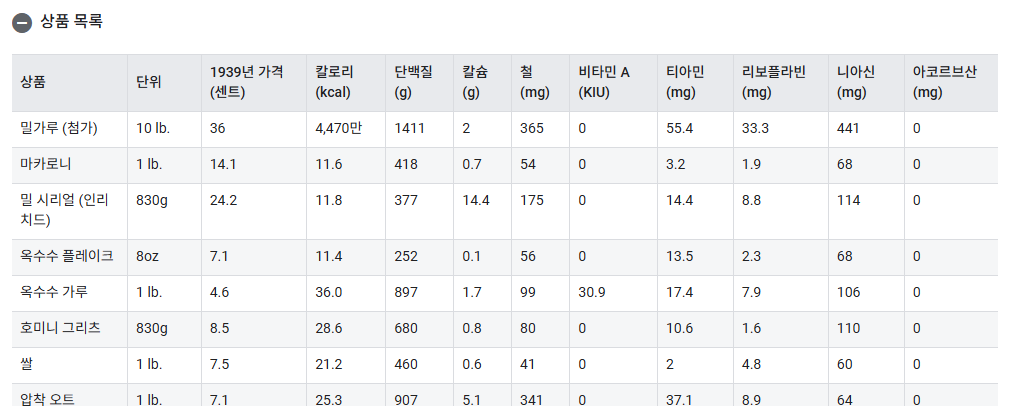
이 문제의 예시에선 제약조건과 목적함수를 1번 항목처럼 사용했다.
영양소에 대한 제약조건을 선언하고, SetCoefficient()를 이용해 각각의 음식과 영양소에 대한 식을 세워준다.
foods가 최적화된 값을 담을 변수들이다.
# 제약조건
constraints = [] # 가격 * 영양소들의 합이 각각의 기준 영양소보다 같거나 커야 함.
for i, nutrient in enumerate(nutrients):
constraints.append(solver.Constraint(nutrient[1], solver.infinity())) # 영양소마다 최소 영향소부터 무한대까지 정의
for j, item in enumerate(data):
constraints[i].SetCoefficient(foods[j], item[i+3]) # 가격 * 영양소
print("Number of constraints =", solver.NumConstraints())
# 목적함수
objective = solver.Objective() # 각 가격을 더한 값
for food in foods :
objective.SetCoefficient(food, 1)
objective.SetMinimization()
나는 2번의 방식으로 문제를 풀어봤다.
비슷하게 리스트에 각각의 음식과 영양소 값을 더한 뒤,
그 배열의 합계가 영양소의 기준보다 같거나 크다는 것을 Add()를 이용해 제약조건으로 넣어주었다.
# 제약조건
for i, nutrient in enumerate(nutrients):
result_mid = []
for j, item in enumerate(data):
result_mid.append(foods[j] * item[i+3])
solver.Add(sum(result_mid) >= nutrient[1])
print("Number of constraints =", solver.NumConstraints())
# 목적함수
solver.Minimize(sum(foods))
선형문제가 아닌 비선형, 이산 문제를 푸는 솔버도 있다.
둘의 해결방법이 다르기 때문에 문제를 잘 이해하고 필요한 솔버를 사용하면 좋을 듯 하다.
참고: https://developers.google.com/optimization/mip/mip_example?hl=ko