[강화학습] 동적계획법 (Dynamic Programming)

카테고리 없음

yennle 2022. 11. 1. 14:01

728x90

이전 글에 이어서 동적계획법에 대해 정리한다.

중첩되는 부분문제들(overlapping subproblems)

- 부문 문제 및 상위 부분 문제의 형태가 동일함.

- 문제의 크기만 변화 (실질적으로 다루고자 하는 문제의 형태는 동일)

- 문제를 정의했을 때, 원래 풀고자 한 문제도 정의가 되어야 함.

한 문제의 최적해는 그 부분 문제의 최적해로부터 구성

부분 문제의 최적해를 이용해 상위 문제 해결

V(i, j)값을 구하기 위해서 V(i, j+1), V(i+1, j)의 최적값을 이용해야 한다.

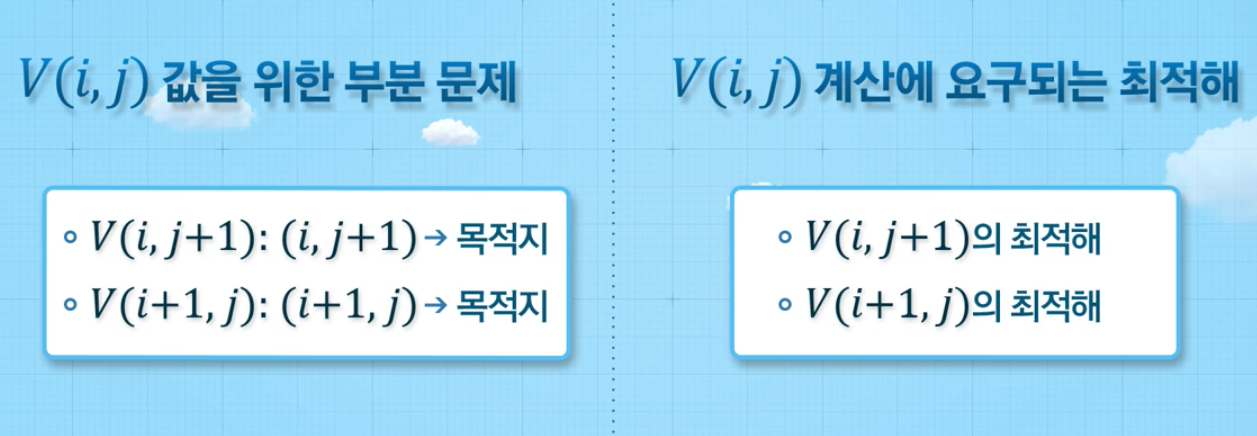
< 최적화의 원리 >
한 문제에 대한 해가 최적이라면 그 문제를 이루는 모든 부분 문제들에 해당하는 부분해가 부분 문제의 최적해

어떤 상태에서 어떤 행동을 결정하면 그 다음 단계의 상태가 확정적으로 결정되는 경우

각 문제는 여러 단계(stage) 혹은 의사결정시점(decision epoch)로 나뉨 -> 의사결정을 내리는 시점

각 단계에서는 상태(state)를 바탕으로 의사결정(행동, action)이 이루어짐

$a_t$라는 행동을 했을 때, 다음 상태 $s_{t+1}$은 $f_t()$에 의해 결정이 된다.

또한, 어떤 상태에서 어떤 행동을 하면 그에 따른 보상을 $r_t()$라고 정의한다.

식으로 표현하면 아래와 같다.

$$ s_{t+1} = f_t(s_t, a_t)$$

$$ r_t = r_t(s_t, a_t) $$

$s_0$의 상태에서 $a_0$라는 행동을 취하면 $r_0$의 보상을 받고 $s_1$의 상태로 전이되며, 이 과정을 반복한다.

이제 어떤 행동을 선택할 것인지가 문제 !

즉, 초기 상태 $s_0$가 주어진 상황에서 T기간에 걸친 총 보상합($r_0+ r_1+\cdots+r_{T-1}$)을 최대화하기 위한

일련의 행동들($a_0,\ a_1,\ \cdots,\ a_{T-1}$)을 결정하는 것

Decision rule : 모든 가능한 상태에서 최적의 행동을 찾는 것. $\delta_t(s_t) = a_t$

Policy : 모든 단계에서의 decision rule의 집합. $\pi = \left\{ \delta_t \right\}_{t=0,1,\cdots ,T-1}$

$v^*_t(s_t)$ : $v_t(x)$시점부터 남은 기간 획득 가능한 총 보상의 최대값

$$ v^*_t(s_t) = \displaystyle \max_{a_t,a_{t+1},\cdots ,a_{T-1}}\left\{r_t+r_{t+1}+\cdots +r_{T-1}\right\} $$

=> 궁극적인 목표는 $v^*_0(s_0)$를 구하는 것.

중첩되는 부분문제를 풀기 위해서는 벨만 최적 방정식을 사용하면 된다.

벨만 최적 방정식 (Bellman Optimality Equation)
$$v^*_t(s_t) = \displaystyle \max_{a_t}\left\{r_t(s_t,a_t)+v^*_{t+1}(f_t(s_t,a_t)) \right\}$$

역진귀납법에 벨만 최적 방정식을 사용하면 $v^*_0(s_0)$를 구할 수 있다.

역진 귀납법이란 가장 마지막 단계에 있는 문제부터 순차적으로 문제를 풀어 나가는 것.

① 모든 가능한 $s_{T-1}$에 대해 $v^*_{T-1}(s_{T-1})=\displaystyle \max_{a_{T-1}}r_{T-1}$을 계산한다.

② $t=T-2,\ T-3,\ \cdots,\ 1$의 순서로 모든 가능한 $s_t$에 대해 $v^*_{t}(s_{t})$를 계산한다.

③ 초기 상태 $s_0$에 대해, $v^*_0(s_0) = \displaystyle \max_{a_0}\left\{r_0(s_0,a_0)+v^*_{1}(s_1) \right\}$을 계산

이는 $ v^*_t(s_t) = \displaystyle \max_{a_t,a_{t+1},\cdots ,a_{T-1}}\left\{r_t+r_{t+1}+\cdots +r_{T-1}\right\} $와 동일

[참고]

728x90