[python] Ridge, Lasso regression 코드 실행하기

 

 

https://www.datacamp.com/tutorial/tutorial-lasso-ridge-regression

위 링크를 참고해 코드를 실행했다.

 

 

데이터는 캐글의 Predict Podcast Listening Time의 데이터를 사용했으며,

숫자데이터만을 이용해서 청취 시간과의 관계를 알아보기 위해 회귀분석을 진행하고자 한다.

https://www.kaggle.com/competitions/playground-series-s5e4

 

 

---

 

 

< 변수 관계 파악 >

먼저 데이터들의 관계를 살펴보았다.

에피소드 별 길이(Episode_Length_minutes)만 유일하게 청취시간(Listening_Time_minutes)와

양의 관계를 가진다는 것을 알 수 있다.

#libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, RidgeCV, Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston


sns.heatmap(df[df.columns[[2, 4, 7, 8, -1]]].sample(10000).corr(), annot = True)

 

 

 

< 전처리 >

회귀 모델을 돌리기 앞서 전처리가 필요하다.

결측치가 있으면 오류가 나기 때문이다.

결측치가 있는 변수를 확인한 후에 결측치가 존재하는 변수에 대해서만 처리해주었다.

# 결측치 확인
df.isnull().sum()

# 결측치 처리(평균값으로 대체)
numerical_cols = ['Episode_Length_minutes', 'Guest_Popularity_percentage', 'Number_of_Ads']
df[numerical_cols] = df[numerical_cols].fillna(df[numerical_cols].median())

 

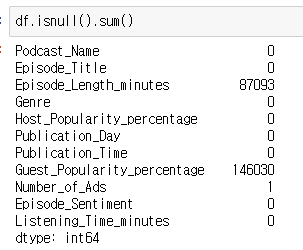전처리 전

전처리 후

 

 

 

 

 

< 데이터 분할와 스케일링 >

모델 학습에 앞서 데이터를 학습데이터와 테스트데이터로 분할한다.

그리고 단위가 다른 변수들의 단위를 동일하게 하기 위해서 스케일링을 진행한다.

#preview
features = df.columns[[2, 4, 7, 8]]
target = df.columns[-1]

#X and y values
X = df[features].values
y = df[target].values

#splot
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=17)

print("The dimension of X_train is {}".format(X_train.shape))
print("The dimension of X_test is {}".format(X_test.shape))
#Scale features
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

 

 

 

 

< LinearRegression >

결과 비교를 위해 선형회귀의 코드도 함께 실행한다.

#Model
lr = LinearRegression()

#Fit model
lr.fit(X_train, y_train)

#predict
prediction = lr.predict(X_test)

#actual
actual = y_test

train_score_lr = lr.score(X_train, y_train)
test_score_lr = lr.score(X_test, y_test)

print("The train score for lr model is {}".format(train_score_lr))
print("The test score for lr model is {}".format(test_score_lr))

 

 

 

< Ridge Regression >

alpha가 정규화항 앞의 가중치를 의미하는 값이다.

모델의 결과는 선형회귀랑 동일하다. 

#Ridge Regression Model
ridgeReg = Ridge(alpha=10)  # ||y - Xw||^2_2 + alpha * ||w||^2_2

ridgeReg.fit(X_train,y_train)

#train and test scorefor ridge regression
train_score_ridge = ridgeReg.score(X_train, y_train)
test_score_ridge = ridgeReg.score(X_test, y_test)

print("\nRidge Model............................................\n")
print("The train score for ridge model is {}".format(train_score_ridge))
print("The test score for ridge model is {}".format(test_score_ridge))

 

 

 

 

선형회귀와 릿지회귀의 결과는 거의 비슷하다.

그래프로 확인하면 변수 별로 같은 영향력을 가진다는 것을 알 수 있다.

plt.figure(figsize = (10, 10))
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#plt.plot(rr100.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'Ridge; $\alpha = 100$')
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
plt.xticks(rotation = 90)
plt.legend()
plt.show()

 

 

 

< Lasso Regression >

라쏘 코드는 다음과 같다. Rigde랑 크게 다른 것은 없으나,

alpha를 이용해 변수 선택을 할 수 있기 때문에 다양한 alpha를 줘서 결과를 봤다.

#Lasso regression model
print("\nLasso Model............................................\n")
lasso = Lasso(alpha = 0.001)
lasso.fit(X_train,y_train)
train_score_ls =lasso.score(X_train,y_train)
test_score_ls =lasso.score(X_test,y_test)

print("The train score for ls model is {}".format(train_score_ls))
print("The test score for ls model is {}".format(test_score_ls))

 

 

 

alpha가 작을 땐 모든 변수의 가중치가 0이 아닌 값을 가진다.

그러나, alpha가 커지면서 가중치가 0이 아닌 값이 생기는 것을 확인할 수 있다.

이렇게 변수 선택을 하는 것!

fig, ax = plt.subplots(2, 3, figsize=(15, 10), sharex=True)

for idx, al in enumerate([0.0001, 0.001,0.01, 0.1, 1, 10]):

    lasso = Lasso(alpha = al)
    lasso.fit(X_train,y_train)
    train_score_ls =lasso.score(X_train,y_train)
    test_score_ls =lasso.score(X_test,y_test)


    pd.Series(lasso.coef_, features).sort_values(ascending = True).plot(kind = "bar", ax=ax[idx//3][idx%3])
    ax[idx//3][idx%3].set_title('alpha = 0.0001')

 

 

 

 

< LassoCV >

lasso에서 가장 적절한 alpha를 선택하는 방법이 있다.

LassoCV라는 함수를 사용한다.

#Using the linear CV model
from sklearn.linear_model import LassoCV

#Lasso Cross validation
lasso_cv = LassoCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10], random_state=0).fit(X_train, y_train)


#score
print(lasso_cv.score(X_train, y_train))
print(lasso_cv.score(X_test, y_test))

 

 

 

선형회귀, Ridge, LassoCV와의 결과를 비교할 수 있다.

#plot size
plt.figure(figsize = (10, 10))
#add plot for ridge regression
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)

#add plot for lasso regression
plt.plot(lasso_cv.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'lasso; $\alpha = grid$')

#add plot for linear model
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')

#rotate axis
plt.xticks(rotation = 90)
plt.legend()
plt.title("Comparison plot of Ridge, Lasso and Linear regression model")
plt.show()