[논문] Are Transformers Effective for Time Series Forecasting? (2022) - 2

 

https://yensr.tistory.com/162

[논문] Are Transformers Effective for Time Series Forecasting? (2022) - 1

 

 

---

 

 

2. Preliminaries: TSF Problem Formulation

 

시계열 예측 문제는 미래의 $T$개의 시점에서의 값을 예측하는 것.

$T >1$인 경우, 예측 방식이 2가지 존재한다.

 

Iterated Multi-Step (IMS) Forecasting

단일 스텝 예측(single-step forecatster)을 학습한 후, 이를 반복해서 적용하는 방식

자기 회귀 추정 방식 사용 -> 분산 작음. but 반복 과정에서의 오차 누적문제 불가피

단일 스텝 예측 모델의 정확도가 높은 경우에 적합. T가 작은 경우

 

Direct Multi-Step (DMS) Forecasting

다중 스텝 예측을 한 번에 최적화해서 진행하는 방식

편향없는 단일 스텝 예측 모델을 얻기 어려운 경우 사용. T가 큰 경우

 

 

 

 

 

3. Transformer-Based LTSF solutions

 

기존 트랜스포머 모델을 LSTF 모델에 적용하는 데는 한계가 존재

1. 셀프 어텐션의 시간, 메모리 복잡도의 이차적인 증가(제곱)

2. 자기회귀적인 디코더 디자인에서 야기되는 오차 누적

 

Informer는 이러한 문제를 다루고,

복잡성이 감소된 새로운 트랜스포머 아키텍처와 DMS 예측 전략을 제안한다.

 

The pipeline of existing Transformer-based TSF solutions.

 

 

< Time series decomposion 시계열 분해 >

데이터 전처리 과정에서, TSF는 평균을 0으로 맞추는 정규화가 일반적으로 사용됨.

 

Autoformer라고 하는 트랜스포머 기반 모델은 seasonal-trend 계절-추세 분해를 적용

=> 원시 데이터를 보다 예측 가능하게 만들기 위한 시계열 분석의 표준적인 방법

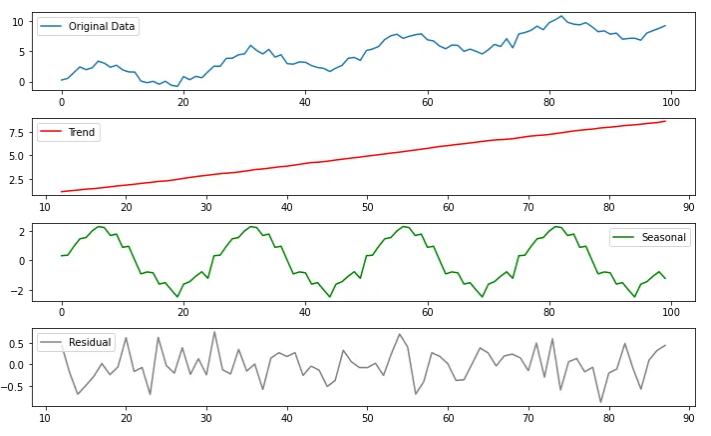
• 입력시퀀스에 이동평균 커널을 적용해 추세-주기 성분을 추출
• 원래 시퀀스에서 추세 성분을 뺀 것을 '계절 성분'으로 간주

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

# 시계열 데이터 생성 (예: 100일 동안의 매일 데이터)
np.random.seed(42)
time = np.arange(100)
trend = time * 0.1  # 선형적인 증가 추세
seasonality = 2 * np.sin(time * (2 * np.pi / 25))  # 25일 주기의 계절성
noise = np.random.normal(scale=0.5, size=len(time))  # 노이즈 추가
data = trend + seasonality + noise  # 전체 시계열 데이터

# 데이터프레임으로 변환
df = pd.DataFrame({'Time': time, 'Value': data})
df.set_index('Time', inplace=True)

# 시계열 분해 수행 (이동 평균 사용)
decomposition = seasonal_decompose(df, model='additive', period=25)

# 그래프 출력
plt.figure(figsize=(10, 6))
plt.subplot(4, 1, 1)
plt.plot(df, label='Original Data')
plt.legend()

plt.subplot(4, 1, 2)
plt.plot(decomposition.trend, label='Trend', color='red')
plt.legend()

plt.subplot(4, 1, 3)
plt.plot(decomposition.seasonal, label='Seasonal', color='green')
plt.legend()

plt.subplot(4, 1, 4)
plt.plot(decomposition.resid, label='Residual', color='gray')
plt.legend()

plt.tight_layout()
plt.show()

 

 

FEDformer는 전문가 혼합 전략을 제안

다양한 크기의 이동 평균 커널을 통해 추출된 추세 성분을 혼합하는 방식

 

 

 

 

< Input embedding strategies 입력 임베딩 전략 >

셀프 어텐션은 시계열 데이터의 순서정보를 보존할 수 없다.

그러나, 시간 순서는 매우 중요한 요소다. 전역적인 시간정보(global temporal information)*도 유용하게 작용한다.

*전역적인 시간정보란 주, 월, 연도의 계층적 타임스탬프(hierarchical timestamps)와 공휴일, 특정이벤트 등의 비계층적 타입스탬프(agnostic timestamps)를 의미

 

시계열 입력의 시간적 맥락을 강화하기 위해서 최신 트랜스포머 방법에서는

여러 임베딩을 추가하는 전략을 사용한다.

 

• 고정된 위치 인코딩 (fixed positional encoding)
  • 대표적인 방법이 sin, cos을 이용한 인코딩
  • 학습이 불필요하고, 입력 시퀀스의 길이에 따라 항상 같은 위치 벡터 제공
  • 일반적인 트랜스포머에서 많이 사용
  • 데이터의 주기성(주, 월, 연도) 등을 직접 반영하기 어려움
  • 고정된 값이기 때문에 데이터의 특성을 학습하지 못함.
• 채널 투영 인코딩 (channel projection embedding)
  • 다차원 데이터를 고정된 차원으로 변환하는 방법
  • 온도, 습도, 풍속 등의 센서 데이터를 입력으로 사용
  • 데이터의 특성을 반영해 의미있는 표현을 학습할 수 있음.
• 학습 가능한 시간 임베딩 (learnable temporal embeddings)
  • 특정 시간 정보(요일, 월, 연도 등)을 모델이 직접 학습하는 방법
  • 요일, 공휴일, 월말 등을 학습 가능한 벡터로 변환, 반영
  • 트랜스포머 기반 시계열 모델에서 가장 많이 사용됨
• 시간 합성곱 (Temporal Convolution)
  • CNN은 국소적인 패턴을 잘 학습하는 특성을 가짐.
  • 단기적인 시간 패턴을 효과적으로 학습

 

 

 

[출처 및 참고]

https://arxiv.org/abs/2205.13504