[최적화] Convex Sets

 

 

세가지 종류의 set ( affine set, convex set, cone )에 대해 정리

 

 

line, line segment, ray

$y = \theta x_1 + (1-\theta)x_2$

 

line

직선. 두 점을 지나면서 양쪽 방향으로 무한히 커지는 선. ($\theta \in \mathbb{R}$)

affine set은 line이 모여서 만들어짐.

 

line segment

선분. 두 점 사이에서만 정의되는 선. ($0 \le \theta \le 1$)

convex set은 line segment가 모여서 만들어짐.

 

ray

반직선. 한 점에서 시작해 다른 점을 지나면서 무한히 커지는 선. ($\theta > 0$)

con은 ray가 모여서 만들어짐.

 

 

 

 

 

Affine set

점, 직선, 평면, 초평면과 같이 선형적 특성이 있으면서 경계가 없는 집합

$C \subseteq R^n$ 에 속한 두 점 $x_1, x_2 \in C$ 을 지나는 직선을 만들었을 때, 이 직선이 C에 포함되는 집합

 

$\theta x_1 + (1-\theta)x_2 \in C$ with $\theta \in \mathbb{R}$

 

두 점을 선형결합*했다고 할 수 있음. 그리고 두 점의 계수의 합은 1

*선형결합(linear combination) : 각 항에 상수를 곱하고 더한 것.

 

 

 

affine combination

 

여러 점들을 linear combination 할 때 계수의 합을 1로 제한한 것

 

$\theta_1x_1+\theta_2x_2+\cdots+\theta_kx_k \in C$  with  $\theta_1+\theta_2+\cdots+\theta_k = 1$

 

어떤 집합에 속하는 점들을 affine combination했을 때 그 결과가 다시 그 집합에 속하면

그 집합은 affine set이라고 할 수 있다.

반대도 마찬가지

 

 

 

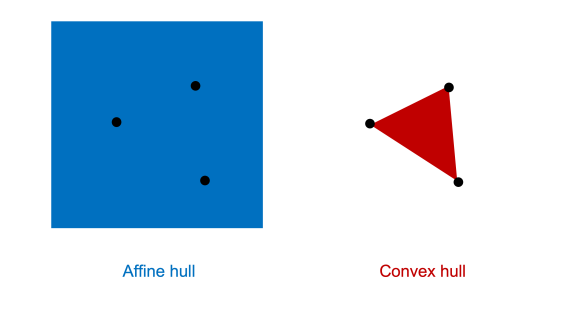
affine hull

 

$C \subseteq \mathbb{R} ^n$ 에 포함된 점들의 모든 affine combination들의 집합을 C의 affine hull이라고 함.

aff C는 항상 affine set이며, 집합 C를 포함하는 가장 작은 affine set

 

$aff(C) = \{{ \theta_1x_1+\theta_2x_2+\cdots+\theta_kx_k \ | \ x_1, \cdots, x_k \in C, \theta_1+\cdots+\theta_k = 1\}}$

 

 

 

 

convex set

$C \subseteq R^n$ 에 속한 두 점 $x_1, x_2 \in C$ 을 지나는 line segment가 C에 포함되는 집합

 

$\theta x_1 + (1-\theta)x_2 \in C$ with $x_1, x_2 \in C$, $0 \le \theta \le 1$

 

 

 

convex combination

 

점들을 linear combination 할 때 계수가 양수고 합을 1로 제한한 것

 

$\theta_1x_1+\theta_2x_2+\cdots+\theta_kx_k \in C$  with  $\theta_1+\theta_2+\cdots+\theta_k = 1 ,\ \theta_i \ge 0, \ i=1,\cdots,k$

 

 

 

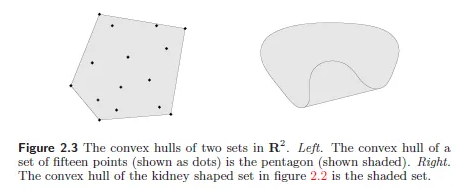
convex hull

 

$C \subseteq R^n$ 에 포함된 점들의 모든 convex combination들의 집합을 C의 convex hull이라고 함.

 

$aff(C) = \{{ \theta_1x_1+\theta_2x_2+\cdots+\theta_kx_k \ | \ x_i \in C,\theta_i \ge 0, \ i=1,\cdots,k, \ \theta_1+\cdots+\theta_k = 1\}}$

 

출처 : https://statisticaloddsandends.wordpress.com/2022/11/18/affine-hull-vs-convex-hull/

 

 

cone

원점에서 시작해서 집합에 속한 점 x \in C을 지나는 ray를 만들었을 때,

$\theta x \in C$가 되면 C는 cone 또는 nonnegative homogenuos라고 함.

 

$\theta x \in C$ with $x \in C,\ \theta \ge 0$

 

cone은 반드시 원점을 포함해야 함.

 

 

 

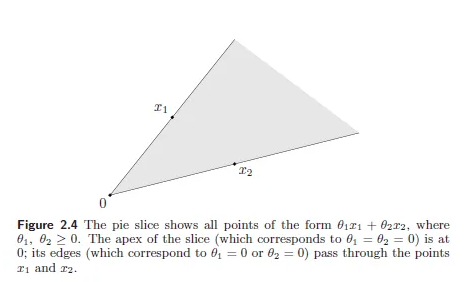
convex cone

 

집합 C가 cone이면서 동시에 convex인 경우

$\theta_1 x_1 + \theta_2 x_2 \in C$ with $x_1, x_2 \in C, \ \theta_1, \theta_2 \ge 0$

 

 

 

conic combination

 

여러 점들을 linear combination할 때, 계수를 0이상으로 제한한 것.

$\theta_1x_1+\theta_2x_2+\cdots+\theta_kx_k$  with  $\theta_i \ge 0, \ i=1,\cdots,k$

 

 

 

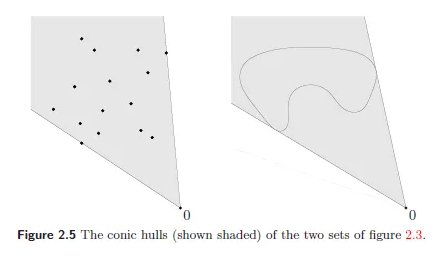
conic hull

 

$C \subseteq \mathbb{R} ^n$에 포함된 점들의 모든 convex combination들의 집합을 C의 convex hull이라고 함.

$\{{ \theta_1x_1+\theta_2x_2+\cdots+\theta_kx_k \ | \ x_i \in C,\theta_i \ge 0, \ i=1,\cdots,k\}}$

 

 

 

 

 

 

[출처 및 참고]

https://web.stanford.edu/~boyd/cvxbook/

https://convex-optimization-for-all.github.io/

https://wikidocs.net/book/1896