[논문] Attention Is All You Need (2017) - 3

 

 

3.3. Position-wise Feed-Forward Networks

 

인코더, 디코더의 각각의 레이어는 각 포지션에 따로 그리고 동일하게 적용되는

'fully connected feed-forward network 완전 연결 피드 포워드 네트워크'를 포함한다.

FFN은 두 번의 선형 변환과 그 사이 ReLU 활성화로 구성된다.

 

$$FFN(x)=max(0,x{W}_1+b_1)W_2+b_2$$

 

 

 

 

선형 변환이 다른 위치에서 동일하게 일어나지만, 각 층마다 다른 파라미터를 사용함.

이것은 커널 사이즈가 1인 두 개의 컨볼루션이라고 묘사할 수 있음.

 

선형 변환과 커널 사이즈 1인 컨볼루션

 

사진의 가운데 2X2의 행렬이 커널.

커널 사이즈가 1이면 저 출력(노란색 행렬)도 입력(파란색 행렬)과 같이 3X3의 크기를 가지게 됨.

여기서, 커널이 1X1이면 입력에 가중치가 곱해진 형태로 출력이 나오게 되는데, 그것이 선형 변환임.

 

출처 : https://wikidocs.net/64066

 

 

입력과 출력의 차원은 $d_{model} = 512$이고 내부 레이어의 차원은 $d_{ff}=2048$

 

입력 문장의 길이를 $seq\_len$이라고 하면

multi-head attention의 결과값인 행렬의 크기는 $(seq\_len, d_{model})$

첫 번째 가중치 행렬의 크기는 $(d_{model}, d_{ff})$

그럼, 첫 번째 선형 변환의 결과의 크기는 $(seq\_len, d_{ff})$

 

ReLU 활성화 함수를 거친 뒤, 두 번째 선형 변환 입력값의 크기는 $(seq\_len, d_{ff})$

두 번째 가중치 행렬의 크기는 $(d_{ff}, d_{model})$

따라서, 두 번째 선형 변환의 결과의 크기는 $(seq\_len, d_{model})$

 

 

 

 

 

3.4. Embeddings and Softmax

입력값 토큰과 출력값 토근을 $d_{model}$의 차원으로 만드는데, 학습된 임베딩 사용

또한, 디코더의 출력값을 predicted next-token probabilities예측된 다음 토큰 확률로 변환하기 위해

선형 변환과 소프트맥스 함수를 사용함.

 

두 개의 임베딩 레이어와 소프트맥스 전의 선형 변환은 동일한 가중치 행렬을 공유한다.

(Using the output embedding to improve language models 논문에서 제안한 방식과 유사)

임베딩 레이어에서는 가중치에 $\sqrt{d_{model}}$를 곱해서 사용한다.

 

 

 

 

 

3.5. Positional Encoding

 

트랜스포머는 반복과 컨볼루션이 없기 때문에, 모델이 시퀀스의 순서를 이용하기 위해서는

시퀀스 내에서 토큰의 상대적이고 절대적인 위치에 대한 약간의 정보를 주입시켜야 함.

=> "Positional Encoding"을 인코더, 디코더 아래 input embedding에 추가

 

포지셔널 인코딩은 임베딩과 동일한 차원 $d_{model}$을 가짐

그래서 합(+)이 가능한 것.

 

 

 

 

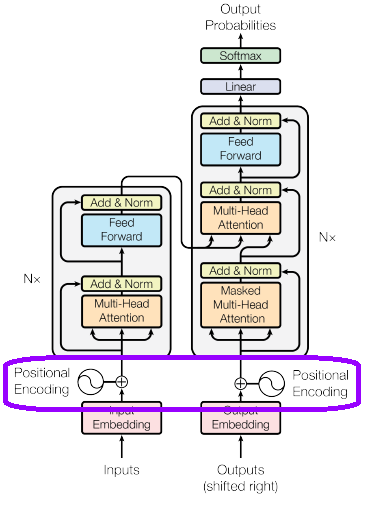
포지셔널 인코딩은 learned positional encoding과 fixed positional encoding 등 다양한 방식이 있음.

( Convolutional sequence to sequence learning 논문 참고)

 

 

이 연구에서는 다른 주파수의 사인, 코사인 함수를 이용

$$\begin{array}{r}P{E}_{(pos,2i)}=sin(pos/{10000}^{2i/d_{model}})\\ P{E}_{(pos,2i+1)}=cos(pos/{10000}^{2i/d_{model}})\end{array}$$

 

$pos$는 위치고, $i$는 차원

이 주파수는 $2\pi$부터 $10000*2\pi$까지 기하급수적으로 증가

=> 고정된 오프셋 $k$에 대해 $PE_{pos+k}$는 $PE_{pos}$의 선형 함수로 표현 가능

=> 모델 상대적인 위치로부터 주의를 기울이게 하는 것을 쉽게 학습함.

말이 어색하지만, 아무튼 모델이 위치정보도 얻을 수 있다는 것을 의미

출처 : https://wikidocs.net/31379

 

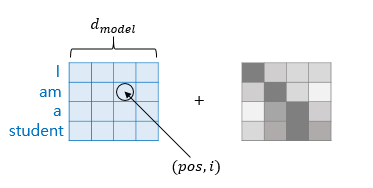
< 예시 >

위치($pos$)가 2, 차원($i$)이 2면

$PE_{(2, 2)} = sin(2/10000^{2*1/d_{model}})$

위치($pos$)가 2, 차원($i$)이 5면

$PE_{(2, 3)} = cos(2/10000^{2*1/d_{model}})$

 

참고 링크 : https://tigris-data-science.tistory.com/entry/%EC%B0%A8%EA%B7%BC%EC%B0%A8%EA%B7%BC-%EC%9D%B4%ED%95%B4%ED%95%98%EB%8A%94-Transformer5-Positional-Encoding

 

learned positional encoding도 실험해봤고, 결과가 거의 동일했으나,

사인곡선의 버전이 학습에서 만난 것보다 더 긴 시퀀스의 길이에 대한 추론이 가능.

 

 

 

 

 

[출처 및 참고]

https://arxiv.org/abs/1706.03762

https://wikidocs.net/31695

https://tech.kakaoenterprise.com/45

https://wikidocs.net/228835

https://wikidocs.net/137253

https://tunz.kr/post/4

https://tigris-data-science.tistory.com/entry/차근차근-이해하는-Transformer5-Positional-Encoding