Just Fighting
[개념 정리] 나이브 베이즈 (Naive Bayes) 본문
나이브 베이즈 알고리즘은 주어진 결과에 대해 예측변수 값을 관찰할 확률을 사용하여,
예측변수가 주어졌을 때, 결과 Y=i를 관찰할 확률을 추정한다.
즉, 사건 Y가 일어났을 때 사건 X가 관측될 확률을 이용하여
사건 X가 관측됐을 때 사건 Y가 일어날 확률을 추청하는 것이다.
나이브 베이즈에 대해서 공부를 하기 위해서는 먼저 알아야 하는 개념들이 있다.
< 조건부 확률 >

< 전확률 법칙 >
두 사건 A, B가 있다고 한다면
A는 B에 속하는 부분과 B에 속하지 않는 부분으로 나누어진다.
여기에 조건부 활용을 사용한다면 A의 확률은 아래 식과 같이 나타낼 수 있다.
즉, 사건 A의 확률은 B가 발생했을 때의 A가 일어날 확률과
B가 발생하지 않았을 때 A가 일어날 확률의 가중평균이다.
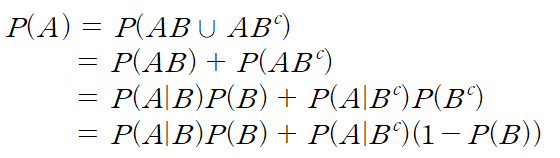

이번에는 사건 A와 B1부터 Bn까지 n개의 사건이 있다고 해보자.
B1, B2,..., Bn이 서로소이고, Bi의 합집합이 전체집합이면 다음 식이 성립한다.
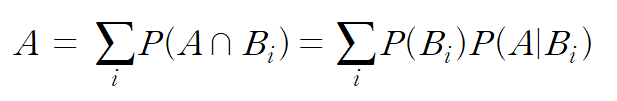
이것을 '전확률 법칙'이라고 한다.
< 베이즈 정리(Bayes' theorem) >
실제 사건이 일어났을 때, 원인의 확률을 구하는 것.
기존의 사건들의 확률을 알고 있다면, 어떤 사건이 일어났을 때 각 원인들의 조건부 확률을 알 수 있다는 것.
P(A) > 0 이면 아래 식이 성립하고, 이것을 '베이즈 정리(Bayes' theorem)'라고 한다.

< 나이브 베이즈(Naive Bayes) >
나이브 베이즈는 베이즈 정리에 기반하고, 변수 간 조건부 독립을 가정한다.
'모든 특징들은 분류 변수의 값이 주어졌을 때 서로 독립이다.' 라고 가정.
베이즈 정리에 따라 어떤 사건들(x)이 일어났을 때, y라는 결과가 나올 확률을
다음 식과 같이 구할 수 있다.

이 때, 조건부 독립을 가정한다면 위의 식이 아래 식처럼 바뀌게 된다.


위의 식에서 우리가 구하고자 하는 확률(왼쪽 항)이 오른쪽항의 분모와 비례한다는 것을 알 수 있으며,
그 분모를 가장 크게하는 y값을 예측값으로 정한다는 의미가 된다.
이 때, P(y)는 사건 Y가 일어날 확률을 의미하고, P(xi|y)는 확률 분포 함수가 들어가게 된다.
(참고 : https://minicokr.com/27)

[참고]
최기헌, 「R을 활용한 확률론 입문」, 자유아카데미(2015)
피터 브루스, 앤드루 브루스, 「데이터 과학을 위한 통계」, 한빛미디어(2018)
H. Zhang (2004). The optimality of Naive Bayes. Proc. FLAIRS.
'ML & DL' 카테고리의 다른 글
| RNN 개념정리 (0) | 2022.07.24 |
|---|---|
| [PySpark] 나이브 베이즈 실습 (0) | 2022.06.09 |
| LSTM을 이용한 텍스트 생성 연습(2) - 모델 생성 (2) | 2022.06.02 |
| LSTM을 이용한 텍스트 생성 연습(1) - 데이터 전처리 (0) | 2022.06.01 |
| [개념 정리] 의사 결정 나무 (0) | 2022.05.03 |




